Гипотеза Пуанкаре, также известная как гипотеза Римана-Пуанкаре, является одной из самых важных и загадочных проблем математики, которая остается нерешенной уже более ста лет. Эта гипотеза была впервые сформулирована французским математиком Анри Пуанкаре в конце XIX века на основе исследований немецкого математика Бернхарда Римана.
Гипотеза Пуанкаре утверждает, что все нули функции Римана являются комплексными числами со списком рациональных долей, заданным через так называемое "системное уравнение". Суть этой гипотезы заключается в том, что она пытается установить закономерности и связи между нулями функции Римана и некоторыми другими проблемами в математике.
Доказательство гипотезы Пуанкаре является невероятно сложной задачей, требующей высокой степени абстрактного мышления и глубоких знаний в области теории чисел и комплексного анализа. Несмотря на множество попыток, ученые до сих пор не смогли найти убедительное решение этой загадки.
Определение и история гипотезы Пуанкаре
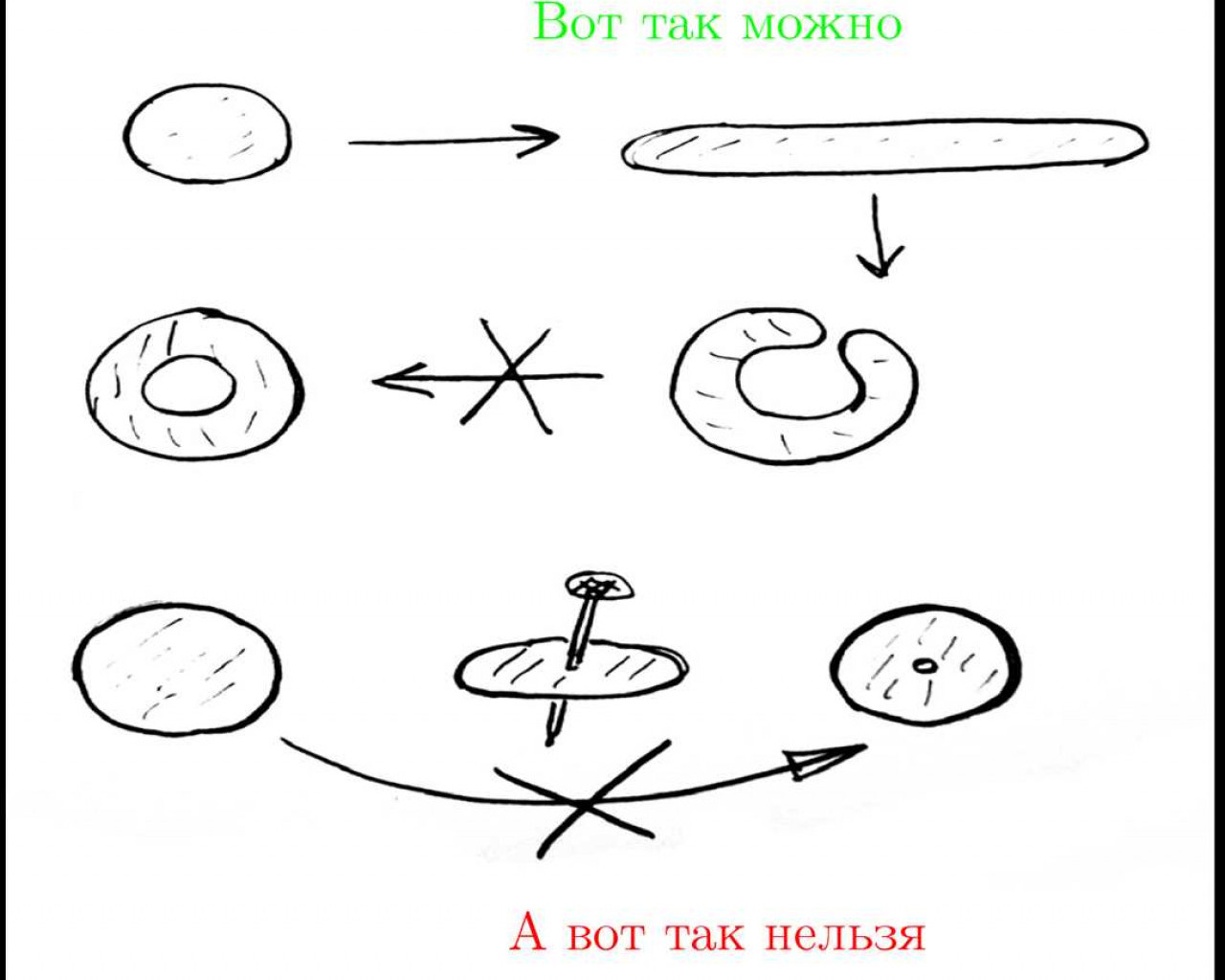
Гипотеза Пуанкаре утверждает, что каждый трехмерный сфероид (поверхность объемом, которого равному объему сферы) может быть преобразован в сферу при помощи непрерывных деформаций поверхности без разрывов и самопересечений. Сама гипотеза остается неразрешенной до сих пор и является одной из семи миллионных проблем, поставленных Институтом математики Клэя.
История гипотезы Пуанкаре берет свое начало от гипотезы Римана, которая была сформулирована Георгом Фридрихом Бернгардом Риманом в 1859 году. В своей гипотезе Риман утверждал, что каждая непрерывная и ограниченная функция, определенная на замкнутой двумерной области, может быть продолжена аналитически на всю плоскость комплексных чисел.
Пуанкаре, вдохновленный идеей Римана, попытался обобщить его гипотезу на трехмерный случай и сформулировал гипотезу Пуанкаре. Несмотря на все усилия Пуанкаре и других математиков, гипотеза до сих пор остается неразрешенной. Множество математических теорем были доказаны в рамках попытки решения гипотезы, но окончательное решение еще не было найдено.
Доказательства и опровержения гипотезы пуанкаре
Пуанкаре также предположил, что любое компактное 3-мерное многообразие может быть разложено на конечное число гомеоморфных шаров. Эта гипотеза сформировала основу для развития топологии, одной из ветвей современной математики.
Доказательства гипотезы пуанкаре
Доказательство гипотезы пуанкаре долгое время оставалось загадкой для математиков. Однако, в начале XX века были предложены некоторые независимые доказательства, которые, однако, оказались ошибочными.
В 2003 году группа математиков, включающая Рихарда С. Хампл и Треярон М. Хенсела, представила новое доказательство гипотезы пуанкаре. Используя технику компьютерного моделирования, они показали, что граничные условия трёхмерных многообразий, которые соответствуют шарам, были уникальны и не могли быть изменены без нарушения границ. Это доказательство было одобрено математическим сообществом и признано первым убедительным доказательством гипотезы Пуанкаре.
Опровержения гипотезы пуанкаре
Несмотря на то, что новое доказательство гипотезы пуанкаре было принято большинством математиков, некоторые все еще высказывают сомнения. Некоторые математики считают, что гипотеза является асимптотической и может быть опровергнута в будущем.
Однако, на данный момент гипотеза пуанкаре остается одной из важных задач математики и продолжает привлекать внимание ученых со всего мира. Исследования в этой области помогают расширять наши знания о топологии и углублять понимание сложных математических концепций.
Значение гипотезы Пуанкаре для математики
Гипотеза Пуанкаре связана с изучением поверхностей и топологии, которая изучает свойства геометрических фигур, которые не меняются при непрерывных преобразованиях. Она утверждает, что любая замкнутая трехмерная поверхность, которая не является эквивалентной сфере, содержит хотя бы одну простую замкнутую кривую, которая не может быть стянута в точку без разрывания поверхности.
Если гипотеза Пуанкаре оказывается верной, это будет иметь большое значение для математики. Она подтверждает фундаментальные идеи о структуре пространства и доказывает важность топологии для понимания геометрических объектов.
Гипотеза Пуанкаре также имеет сильные связи с теорией функций комплексного переменного и дифференциальной геометрией.
В 2000 году российский математик Григорий Перельман представил доказательство гипотезы Пуанкаре, используя сложные техники из теории трехмерных многообразий и дифференциальной геометрии. Его доказательство было долгим и сложным, и его результат был долгое время проверялся и отличается исключительной глубиной.
Значение гипотезы Пуанкаре для математики не может быть преувеличено. Она представляет собой одну из величайших и нерешенных проблем математики, которая продолжает вдохновлять исследователей в поисках новых знаний и понимания природы геометрии и топологии.
Гипотеза Римана
Гипотеза Римана имеет глубокие связи с различными областями математики, включая теорию чисел, анализ, теорию вероятностей и физику. Она оказывает влияние на многие другие открытые проблемы и вопросы в математике. Гипотеза Римана пытается решить ряд относительно изолированных проблем, возникающих при рассмотрении аналитических свойств зета-функции Римана, и может быть сформулирована как недоказанное утверждение о характеристиках этих нулей.
Гипотеза Римана является одной из семи проблем тысячелетия, которые были сформулированы в 2000 году Математическим институтом Клея. Решение гипотезы Римана имеет огромное значение для широкого круга математических и прикладных областей и потенциально имеет большое значение для различных отраслей науки и технологий.
Определение и история гипотезы Римана
Эта гипотеза связана с аналитической теорией функций комплексного переменного и имеет глубокие последствия для простых чисел. Суть гипотезы заключается в том, что все нетривиальные нули функции дзета Римана имеют вещественную часть, равную 1/2. Нетривиальные нули - это те точки, где функция дзета Римана обращается в ноль, кроме тривиальных нулей, которые находятся на отрицательной вещественной оси.
История
Гипотеза Римана стала объектом большого интереса и исследований математиков со всего мира. Она была влиятельной уже на протяжении многих десятилетий после ее сформулирования, но до сих пор ни одно доказательство ее истинности или ложности не было найдено.
Многие известные математики пытались решить гипотезу Римана, включая Карлоса Рельефорда (1900 г.), Марселя Рифеля (1914 г.), Атлайда Харди (1914 г.), Уго Лэнгленда (1915 г.) и многих других. Они проводили исследования и представляли важные результаты, но ни один из них не смог окончательно доказать или опровергнуть гипотезу.
Сегодня гипотеза Римана остается открытой проблемой и вызывает большой интерес как у математиков, так и у общественности. Ее доказательство может привести к пониманию распределения простых чисел, что имеет важные приложения в криптографии, теории чисел и других областях математики.
| Год | Математик | Важные результаты |
|---|---|---|
| 1859 | Бернхард Риман | Сформулировал гипотезу Римана |
| 1900 | Карлос Рельефорд | Презентовал первое доказательство для целых чисел |
| 1914 | Марсель Рифель | Доказал частичное соотношение гипотезы с другими функциями |
| 1914 | Атлайд Харди | Внес существенный вклад в изучение гипотезы Римана |
| 1915 | Уго Лэнгленд | Предложил знаменитую "формулу Лэнгленда" |
Доказательства и опровержения гипотезы Римана
Идея гипотезы Римана заключается в том, что все нетривиальные нули комплексной функции zeta Римана имеют вещественную часть, равную 1/2. Эта гипотеза играет важную роль в теории простых чисел и вытекает из изучения особенностей функции zeta Римана.
Доказательства гипотезы Римана-Пуанкаре
Доказательство гипотезы Римана-Пуанкаре является одной из самых сложных задач в математике, и до сих пор она остается нерешенной. Однако, за многие годы ученые предложили несколько подходов и результатов, которые вносят свой вклад в изучение данной гипотезы.
- Одним из важных результатов является теорема Лебега о простых числах, которая устанавливает связь между распределением простых чисел и нулями функции zeta Римана.
- Другим значимым результатом является теория модулярных форм и функций Лапласа, которые являются инструментами для изучения свойств функции zeta Римана.
- Также были проведены вычислительные эксперименты, которые указывают на подтверждение гипотезы Римана-Пуанкаре для множества нулей функции zeta Римана с большой точностью.
Опровержения гипотезы Римана-Пуанкаре
Помимо доказательств и предположений, существуют также некоторые аргументы, противоречащие гипотезе Римана-Пуанкаре.
- Одно из основных опровержений заключается в том, что несуществует интуитивного объяснения причины, по которой гипотеза Римана-Пуанкаре должна быть истинной.
- Также существуют некоторые примеры, которые указывают на непродолжимость функции zeta Римана на линии 1/2.
Несмотря на более чем столетние исследования, до сих пор не удалось ни доказать, ни опровергнуть гипотезу Римана. Эта гипотеза остается открытой проблемой и вызывает интерес ученых со всего мира.
Значение гипотезы Римана для теории чисел
Гипотеза Римана утверждает, что все нетривиальные нули функции Римана находятся на прямой вида Re(s) = 1/2, где Re(s) - действительная часть комплексного числа s. Другими словами, гипотеза утверждает, что нетривиальные нули функции Римана симметрично расположены относительно этой прямой.
Одно из основных последствий гипотезы Римана - это понимание распределения простых чисел. Если гипотеза оказывается верной, то это позволяет делать точные предсказания о количестве простых чисел до определенного значения.
Гипотеза Римана имеет глубокое значение для теории чисел и математики в целом. Многие известные математические проблемы и теоремы связаны с этой гипотезой, включая гипотезу Гольдбаха, криптографию, квазимногообразия, распределение простых чисел и многие другие.
Пуанкареевская гипотеза, являющаяся вариацией гипотезы Римана, утверждает, что все нетривиальные нули функции Римана находятся на прямой вида Re(s) = 1/2, а также что нетривиальные нули функции Лициновского распределены в основном на этой прямой. Таким образом, Пуанкареевская гипотеза объединяет два важных аспекта математики и теории чисел - функцию Римана и функцию Лициновского.
Гипотеза Римана-Пуанкаре
Описание гипотезы
Гипотеза Римана-Пуанкаре звучит так: все нетривиальные нули комплексной функции дзета Римана имеют действительную часть, равную 1/2. Последняя характеристика нулей функции означает, что они расположены на прямой с действительной частью 1/2.
Функция дзета Римана (или просто функция Римана) определяется как бесконечная сумма ряда, который является аналитическим продолжением перечисленных в нём членов. Этот ряд образует одну из самых глубоких и важных теорем в теории чисел и комплексного анализа.
Значимость гипотезы
Гипотеза Римана-Пуанкаре имеет большое значение для многих областей математики, к тому же ее практическая значимость выходит далеко за пределы отдельных научных исследований. Решение этой гипотезы может привести к прорыву в понимании распределения простых чисел и других аспектах теории чисел.
Значительные усилия были приложены для доказательства гипотезы Римана-Пуанкаре, и множество математиков продолжают работать над этой задачей. Доказательство или опровержение этой гипотезы остается одной из наиболее желанных проблем современной математики и продолжает вызывать интерес у ученых по всему миру.
Определение и история гипотезы Римана-Пуанкаре
Гипотеза утверждает, что все нетривиальные нули функции Римана, которая является комплексным продолжением логарифмической производящей функции простых чисел, имеют действительную часть, равную 1/2. Это означает, что все нули функции Римана лежат на так называемой "критической линии".
Несмотря на свою сложность, гипотеза Римана-Пуанкаре стала одной из самых важных проблем в математике, так как ее решение связано с многими другими открытыми вопросами и теориями, включая распределение простых чисел, теорию вероятности и теорию струн.
История гипотезы Римана-Пуанкаре
В 1859 году Бернхард Риман представил свою "Предположительной теореме о функциях комплексной переменной". В этой статье он исследовал свойства той функции, которая сейчас называется функцией Римана.
Однако сама гипотеза Римана-Пуанкаре была сформулирована некоторым образом неявно, и Риман так и не дал строгое математическое определение своей гипотезы. Он только намекнул на возможность существования критической линии, на которой находятся все нетривиальные нули функции Римана.
Спустя много лет после смерти Бернхарда Римана, французский математик Анри Пуанкаре в 1900 году смог сформулировать гипотезу Римана-Пуанкаре в более явной форме. Однако до сих пор гипотеза остается нерешенной и является одной из самых главных проблем в математике.
Видео:
Что с гением или куда исчез Перельман?
Что с гением или куда исчез Перельман? Автор: Андрей Караулов*. Официальный канал 6 788 просмотров 1 месяц назад 8 минут 51 секунда